The general state of a qubit \(|q\rangle\)

$$|q\rangle = \alpha|0\rangle + \beta|1\rangle$$

where \(\alpha, \beta \in \mathbb{C}\) (complex number)

• since we cannot measure global phase, we can only measure the difference in phase between the states \(|0\rangle\) and \(|1\rangle\)

• Instead of complex number, confine them to the real numbers and add a term to tell us the relative phase between them:

  $$|q\rangle = \alpha|0\rangle + e^{i\phi}\beta|1\rangle$$

  $$\alpha, \beta, \phi \in \mathbb{R}$$

  • since the qubit state must be normalised: \(\sqrt{\alpha^2 + \beta^2} = 1\)

    ⇒ we can use the trigonometric identity: \(\sqrt{\sin^2{x} + \cos^2{x}} = 1\) to describe the real \(\alpha\) and \(\beta\) in terms of one variable \(\theta\):

    $$\alpha = \cos{\tfrac{\theta}{2}}, \quad \beta=\sin{\tfrac{\theta}{2}}$$

    ⇒ we can describe the state of any qubit using the two variables \(\phi\) and \(\theta\)

    $$|q\rangle = \cos{\tfrac{\theta}{2}}|0\rangle + e^{i\phi}\sin{\tfrac{\theta}{2}}|1\rangle$$

    $$\theta, \phi \in \mathbb{R}$$

Bloch sphere

We can write any normalized (pure) state as \(|\psi\rangle = \cos{\tfrac{\theta}{2}}|0\rangle + e^{i\phi}\sin{\tfrac{\theta}{2}}|1\rangle\) where \(\phi \in [0, 2\pi)\) describe the relative phase and \(\theta \in [0, \pi]\) determines the probability to measure \(|0\rangle , |1\rangle\): \(p(0) = \cos^2\tfrac{\theta}{2}, p(1) = \sin^2\tfrac{\theta}{2}\)

\(\Rightarrow\) all normalized pure state can be illustrated on the surface of a sphere with radius \(|\vec{r}|=1\), which we call the Bloch sphere

\(\Rightarrow\) the coordinates of such a state are given by the Bloch vector $$\vec{r} = \begin{bmatrix}\sin\theta \cos\theta \\ \sin\theta\sin\phi \\ \cos\theta\end{bmatrix} = \begin{bmatrix}x \\ y \\ z \end{bmatrix}$$

For example:

• \(|0\rangle: \theta=0, \phi\) is arbitrary \(\Rightarrow \vec{r} =\begin{bmatrix}0 \\ 0 \\ 1 \end{bmatrix}\)

• \(|1\rangle: \theta=\pi, \phi\) is arbitrary \(\Rightarrow \vec{r} =\begin{bmatrix}0 \\ 0 \\ -1 \end{bmatrix}\)

• \(|+\rangle: \theta=\tfrac{\pi}{2}, \phi =0\) \(\Rightarrow \vec{r} =\begin{bmatrix}1 \\ 0 \\ 0 \end{bmatrix}\)

• \(|-\rangle: \theta=\tfrac{\pi}{2}, \phi =\pi \Rightarrow \vec{r} =\begin{bmatrix}-1 \\ 0 \\ 0 \end{bmatrix}\)

• \(|+i\rangle: \theta=\tfrac{\pi}{2}, \phi = \tfrac{\pi}{2} \Rightarrow \vec{r} =\begin{bmatrix}0 \\ 1 \\ 0 \end{bmatrix}\)

• \(|-i\rangle: \theta=\tfrac{\pi}{2}, \phi = \tfrac{3\pi}{2} \Rightarrow \vec{r} =\begin{bmatrix}0 \\ -1 \\ 0 \end{bmatrix}\)

Visually Representing a Qubit State

If we interpret \(\theta\) and \(\phi\) as spherical coordinates (r=1, since the magnitude of the qubit state, is 1), we can plot any single-qubit state on the surface of a sphere, known as the Bloch sphere.

• we have plotted a qubit in the state \(|{+}\rangle, \theta = \pi/2, \phi=0\)

An important thing to remember about qubits is that we don't care about overall phase. Hence if we have a qubit of the form: $$|\psi\rangle = e^{i\alpha}a|0\rangle + e^{i\beta}b|1\rangle = e^{i\alpha} \left( a|0\rangle + e^{i(\beta-\alpha)}b|1\rangle \right)$$ ⇒ we find the Bloch present of \(a|0\rangle + e^{i(\beta-\alpha)}b|1\rangle \)

Example: Represent the following qubit on Bloch Sphere $$\tfrac{1}{\sqrt{2}}(|0\rangle + |1\rangle)$$

Using \(|q\rangle = \cos{\tfrac{\theta}{2}}|0\rangle + e^{i\phi}\sin{\tfrac{\theta}{2}}|1\rangle\) ⇒ \(\cos{\tfrac{\theta}{2}}= 1/\sqrt 2 , \ e^{i\phi}\sin{\tfrac{\theta}{2}}=1/\sqrt2\)

• \(\cos{\tfrac{\theta}{2}} = \cos{\tfrac{\pi}{4}} = \tfrac{1}{\sqrt2}\)

  ⇒ \(\theta = \tfrac{\pi}{2}\)

• \(\ e^{i\phi}\sin{\tfrac{\theta}{2}}=1/\sqrt2\)

  \(\sin{\tfrac{\theta}{2}} = \sin{\tfrac{\pi}{4}} = \tfrac{1}{\sqrt2}\)

  \(e^{i\phi} = 1\) ⇒ \(\phi =0\) So that $$x = r \sin(\tfrac{\pi}{2}) \cos(0) \\ y = r \sin(\tfrac{\pi}{2}) \sin(0) \\ z = r * \cos(\tfrac{\pi}{2})$$ \(\Rightarrow\) Cartesian Bloch Vector = [1.0, 0, 0]

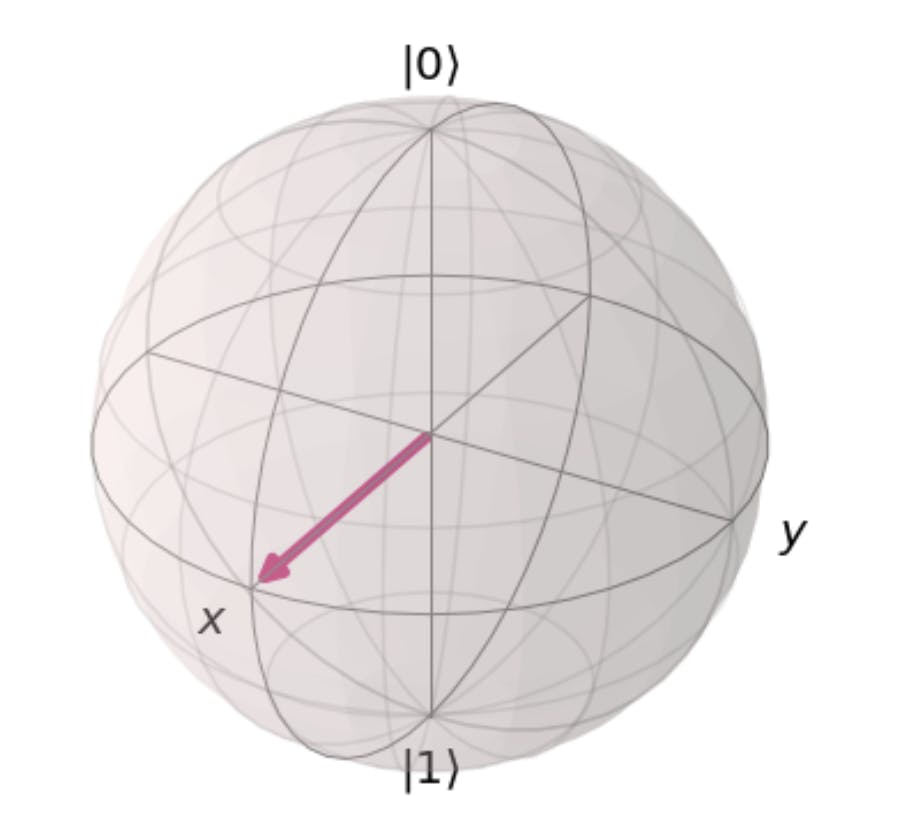
Some common statevectors

Be careful: On the Bloch sphere, angles are twice as big as in Hilbert space e.g. \(|0\rangle , |1\rangle\) are orthogonal, but on the Bloch sphere, their angle is 180^0. For a general state \(|\psi\rangle = \cos{\tfrac{\theta}{2}}|0\rangle + e^{i\phi}\sin{\tfrac{\theta}{2}}|1\rangle \Rightarrow \theta \) is the angle on the Bloch sphere, while \(\tfrac{\theta}{2}\) is the actual angle in Hibert space \(\Rightarrow Z\)-measurement corresponds to a projection onto the z-axis and analogously for X and Y